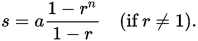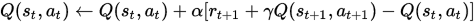Introduction

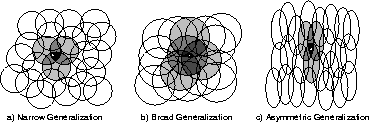
Coarse Coding, such as Tile Coding, is a nice way of storing a model of the environment linear in nature or have an ordinal characteristics (for instance, alphabets are ordinal since it can be ordered: A < B < C, …). The image above illustrates how Coarse Coding may be utilized. a) Narrow Generalization is for problem space where precision over backup speed (samples have to be taken for neighbour values to propagate). b) Broad Generalization is for problem space where generalization can be taken advantage of, making value propagation from neighbours faster.

Problem often occur if our Course Coding model is too fine we want to “Broaden” our model. Before we begin, I’ll discuss a real world problem I encountered recently.

In one of a project with a client, we are given thousands of metrics and ask to solve the following problem:

Given a pattern in a metric, what patterns in other metric entails it. For instance, given a pattern in metric M1 what pattern in other metrics are a culprit or causes it.

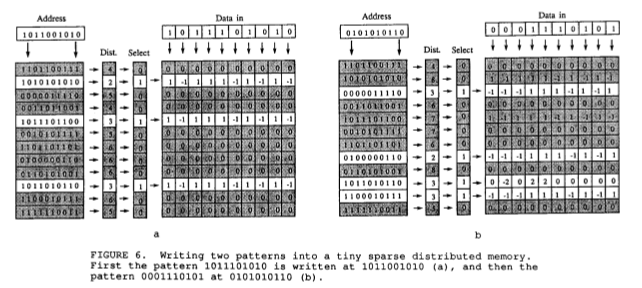
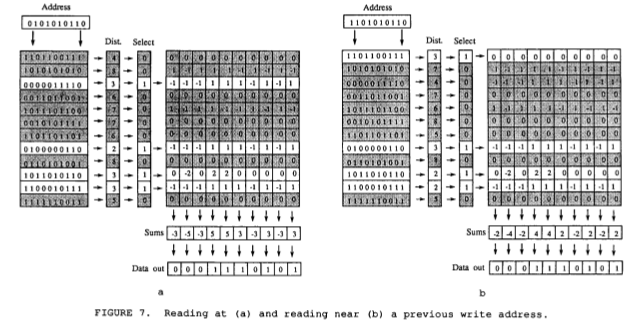
In our project, one of the pattern of interest is a rising web response time metric, and we are asked what entails/causes it? With a little feature engineering, we are able to linearize metrics. By running this through a program that utilizes my rl library, db server response time was found as one of the culprit. These patterns are given below.

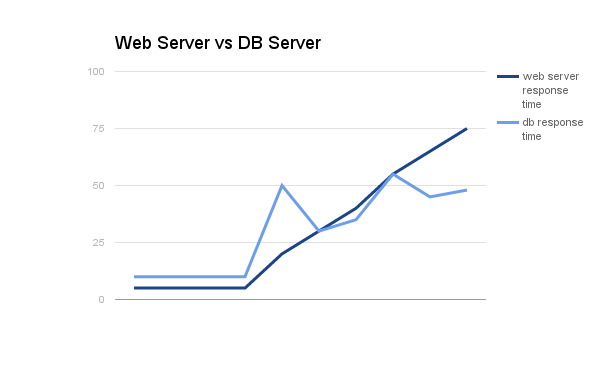
What the program did is basically create a model of the system so that if the db server response time pattern do occur again, we know that it will entail rising response time. An problem arises, it is obvious that db response time don’t have to follow the exact pattern above to entail web response time to rise. That is db response time just have to be elevated around 40-50ms response time for a problem to occur. That is why we want to generalize our model stored in Coarse Coding (specifically Tile Coding).

Solution (Tile Coding)

Although this solution is only for Tile Coding, general idea applies to other types of Coarse Coding. So in our metric above, we want to generalize it to:

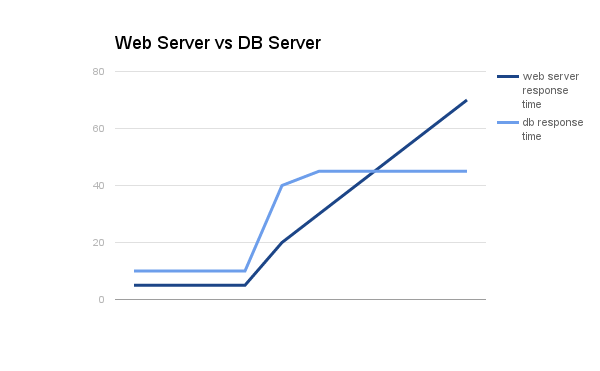
Note on how the bumps are “smoothed out”. This should now give us a better model for this problem. So how do we generalize Tile Codes?

To begin, let us first review a simplified version of Tile Code where it stores a 2D state-action space (1D state and 1D action). Suppose it is stored in the following tile (we will ignore multiple tiling to simplify this further):

Suppose actions are represented by the x axis while the states are represented by the y axis. Generalizing would mean storing the values stored in this grid to the following “Broader Grid”:

Each square in Broad Course Code covers many vertex in the original Course Code. The idea then is each vertex in Broad Coarse Code have a value is the weighted average of all the covered vertex in the original Course Code. This is better illustrated visually here:

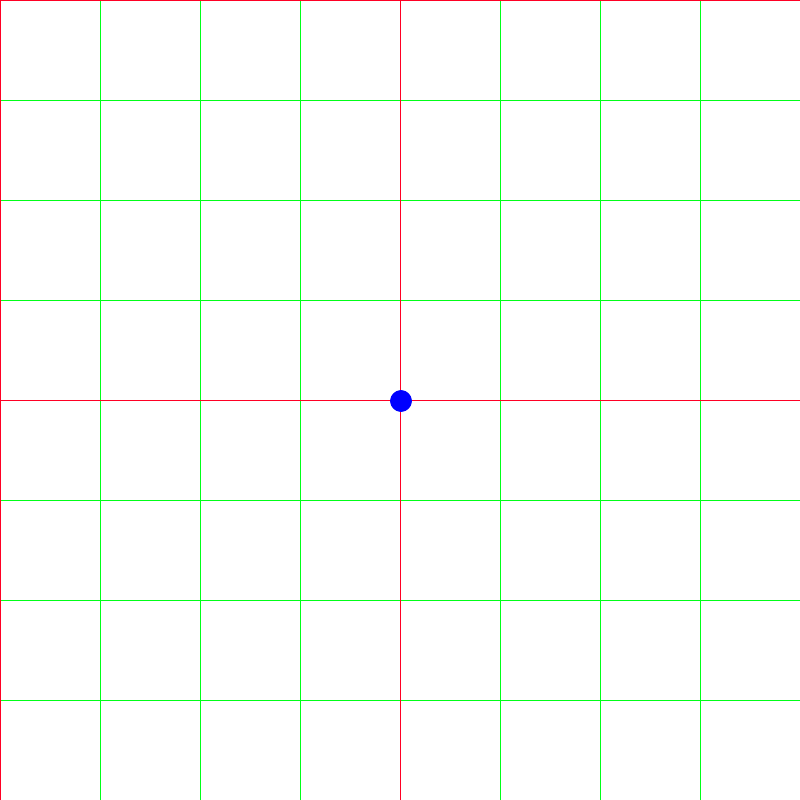
• Let green grid represent the original Tile Code grid.

• Let the red grid represent our wanted Broad Tile Code grid.

• Blue dot be one of the vertex (storage of state-action value) in our new Broad Tile Code grid.

So for the value in the vertex represented by the blue dot, it will be the weighted average of all the green vertex that is under the 4 red squares it sits on. (If vertex is at the side, then the vertex will be sitting on two squares whilst if it is in corner then it will be sitting on just one square). The weights would be the cartesian distance between a green vertex and the blue vertex. The weighted average can easily be done by the following formula:

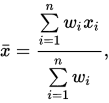
Conclusion

Here we assume that the Tile Coding did not do any hashing. This is an equivalent of using the TileCodeCorrect class in my rl library. Utilizing something with hashing shouldn’t be that big of a deal since the same representation of grids above still holds except that vertex are in “superposition”, in which a vertex is utilized by more than one state-action pair. More sophisticated methods are also needed for “non conventional tiles”:

This method is really helpful in many situations in which discarding precision for myopic view of things is more useful.

Introduction

With my Sparse Distributed Memory (SDM) basic implementation finally done, in which the Up/Down Counters won’t overflow, I’m ready to embark something bigger. At the moment, my implementation stores everything in random-access-memory (RAM), which is very limiting. I have utilize SDM with my reinforcement learning (rl), solving entailments in a set of 11,000 metrics, which occupies all my 16gb of ram. This is not ideal since, even with SDM, there are many collisions, granted they are better than random hashing collision provided by Tile Coding. Also, I can only do machine learning on a smaller and sparse set of data, due to the space. To amend all of this, it is clear what the next step is. Utilize database systems.

The Plan

Since all the “bottleneck” stems from the space requirements of the Up/Down Counters, it makes sense to somehow store all that stuff in database. For a quick review of what Up/Down Counters look like, see the figure below.

What I want is to store each row in database.

Considering that Up/Down Counters row represents a feature vector which is probably not that big, this might be sufficient. Problem occurs if the feature vector is actually huge, then we probably need a smarter way of segmenting each row into cells.

Now we are more robust, allowing us to store bigger data. One thing to note is that storing each row will be faster, due to less “context-switching” when switching to another db entry. Cell solution can do the same by setting the column width to something equal to the size of data. Our final schema is represented by the image below.

• Each UpDownCounter instance have a db entry.

  • Contains the size of each row, DataSize.

• Each UpDownCounter instance have many associated Cell.

  • Contains the ChunkSize of the cell. Although can be saved in UpDownCounter, imagine, having some cell bigger than the other. This should allow for that possibility, although I don’t intend to use it (I don’t mind the redundancy that much).

  • And the data itself, BinData.

  • The row, col stores where this cell is located.

Choosing A Database

Since I don’t intend to uphold the CAP theorem, that is, the possibility of SDM incrementing the same counter at the same time should be possible, and I want horizontal scalability, I must choose one of the NoSQL database. I’ve looked at MongoDB and it’s C++ client (Note, my SDM implementation is in C++) and have found it difficult to build and install. I’ve also looked at Cassandra and it seems like a better fit for my problem. It was easy, way faster, and way scalable.

Conclusion

That’s it! We are done. See you in part 2 when I have a basic working implementation of this.

Introduction

Sparse Distributed Memory (SDM) is a fascinating way of managing exponential growth in memory. As opposed to the traditional random-access memory (RAM) where there is a one to one correspondence between an address and a hard location, SDM can map multiple address to a multiple of hard location. I won’t delve into why this is useful, I suggest reading Mr. Kanerva’s paper, A Cerebellar-Model Associative Memory As A Generalized Random-Access Memory, which I believe is available in IEEE. The purpose of this article is to discuss the shortcoming of writing data in SDM and an amendment from Reinforcement Learning community.

SDM Write/Read operations

Before we delve on addressing the shortcoming, let us quickly review on how the SDM write/read operation works. The figure below is taken from Mr. Kanerva’s paper mentioned above. Again, this is just a quick summary of the write/read operations, thus if lost, consult the paper.

In the paper, it describes the writing of 1011001010 and then 0101010110 to the SDM. Prior to any operations in SDM, the Up/Down Counters or the data storage itself are all zeros. For the first insertion, 1011001010 activated 3 address register in which its Hamming Distance is less than or equal 3. This then updates each cell in activated/selected rows in Up/Down Counters. For instance, all columns aligned to the 1s in 1011001010 are all incremented by one, and all columns aligned to 0s are decremented.

Similar operations occurred for second insertion, 0101010110 but different rows due to different hamming distance less than or equal three are activated.

Reading is by summing all the activated columns. For instance, reading the data addressed by 0101010110 is through summing all the activated columns, resulting in (-3, -5, -3, 5, 5, 3, -3, 3, -3, 3). The sum is finally converted to bits, assigning 0 if the sum of a column is negative, whilst 1 if otherwise. So in our case this is: 0001110101.

Problem with SDM Writing

Now suppose each cell in Up/Down Counter is represented by a 64bit signed integer (to allow for negatives) in a 64bit machine, thus occupying exactly one memory cell. Then there is a scenario in which after 264. Although this may seem like a super worst-case, it’s an overflow we’d rather not have. I have been reading unmentioned implementation and one of it have a try/catch or an if/else guard, considering these write operations happens a lot, this is a significant overhead.

Solution 1: Geometric Series

So our problem is integer overflow. How do we solve this? We want something that is something with a horizontal asymptote, something that slows growing as it approaches a value, all to avoid the overflow.

Geometric series have the following form:

Where a is the initial value, I usually set this to 1 and r is the common ratio. As you can see above, the sum of geometric series is:

If r is set to |r| < 1, then the series converges or “hits” a horizontal asymptote. So how is this useful as a replacement for integers in Up/Down Counters?

Imagine each cell in Up/Down Counters is a double (64bit floating point), a=1, and |r| < 1 (again so we converge), how do we utilized Geometric Series’ converging nature?

• Let R be the current value of a cell.

• Let R’ be the next value of the same cell.

So we acquired R in our nth update. Since it is a geometric series where a=1, and |r| < 1.

R = 1 + r + … + rn

This is not very useful since it assumes we keep track of integer n which defeats the purpose. How can we make a recurrence relationship, that is, how do we get R’ from R? Continuing from formula above:

R = 1 + r + … + rn

R’ = 1 + r + … + rn + rn+1

R’ = 1 + (r + … + rn) x r

R’ = 1 + R x r

To generalize a=1,

R’ = a + R x r

That’s it. That is how we increment our cell in Up/Down Counter. Are we done? How do we decrement?

Solution 2: From Reinforcement Learning

To solve the decrement problem above, we’ll introduce an equation from Reinforcement Learning, specifically, SARSA.

To quickly summarize (you can skip if you want) SARSA, (st, at) is the state-action pair. Q(st, at) is what we are trying to update base on the current observed reward of the next state Q(st+1, at+1). Step-size α controls how fast Q(st, at) learns or converge while 𝛄 dictates how influential future states are. Basically, by shifting rt+1 + 𝛄Q(st+1, at+1) to something greater than Q(st, at), Q(st, at) will be incremented and vice-versa. There lies the idea behind our final solution. If you decompose the equation above, you’ll also unravel a geometric series.

If you don’t care about the SARSA equation above, it’s fine. Basically it allows us to increment/decrement. To make build our final solution, simply replace Q(st, at) as R, or the floating point we are trying to update in our Up/Down counter cell.

R <- R + r[1 - R], for increment

R <- R + r[-1 - R], for decrement

Done! All I can say is shift your common-ratio/step-size to a really small value so you won’t converge quickly. Maybe change 1 to something bigger for the same reason. Other than that, NO MORE OVERFLOW!

Conclusion

Truth be told that the update formula from Reinforcement Learning is not unique. It is everywhere in machine learning literature such as Perceptron Learning Rule and the ever more popular Linear Regression. I just really love Reinforcement Learning that’s why I want to nudge it in.